Before I became a chef and wine geek, I had another career - I was a DC policy wonk. I got my BA and MPA in Washington and I lived and breathed politics. One of my greatest interests was the way studies were touted around town, and I made it my business to study lots of economics and statistics so that I could understand and either support or debunk as needed. I don't have enough training to call myself either an economist or a statistician...but this post requires only the knowledge I learned in my first undergraduate course.
Last week, the American Association of Wine Economists, of which I am a member, released a new Working Paper titled A Buyer's Dilemma - Whose Rating Should a Wine Drinker Pay Attention To? The blogoshpere has paid some attention to this paper, including Terroirist, Eric Levine of Cellartracker, and Vinography.
Basically the findings of the paper are that CellarTracker scores more closely track price point than Parker. Tanzer is sort of in the middle. This is based on a collection of scores and prices for the 2005 vintage in Bordeaux. The implication is that if you are looking at bang for buck, rely on Cellartracker scores (though the authors to their credit do not make this leap, confining their results to the data - 2005 Bordeaux). (Disclaimer -- I subscribe to all three content providers). But the study is sadly and fatally flawed. In my next post, I will go into several reasons why the content of the study may be misleading, but today I want to talk about math.
Bang for Buck
Everyone understands the buck part. The Bang is the thing. Bang, hedonic qualities, juicy goodness, wow factor, number of stars, number of points. Bang is not quantifiable in mathematical terms.
All of math is based on the number line that was stuck to your desk in primary school. 1, 2, 3, 4, etc. The distance between 1 and 2 is 1. The distance between 3 and 7 is 4. You get the idea. There is no rating system in existence that can draw a number line and say the distance, in units of goodness, between wine A and wine B is 12. Furthermore, I have never seen any of them make that claim. Parker gives 50 points just for being alcohol; Tanzer clearly states that his system is based on wow factors and not quantification, and CellarTracker lets people grade in any manner they see fit.
No, wine scores are not, as we say in the industry, interval values, like those we find on a number line. If they were, you could mix a glass with equal parts 92 and 93 point wines and the result would get a 92.5. No, wine scores are ordinal values, where there is a difference between say, 4 and 5 stars, but we can't really quantify that gap. Other examples of ordinal values include military ranks, top ten lists, and the finishing places of runners in a race. The difference between the finishers could be thousandths of a second or hours. The great consequence to social scientists here is that you cannot add, subtract, divide, and multiply ordinal values; and that is exactly what the authors of this paper have done.
The Desire to Quantify
I understand the desire, the need to make things into numbers and then line them up. Social scientists are all alike in this respect, they want some data and they want it to say something about the world. But data in the form of numbers is hard to come by, and way way more often than you might realize, a researcher will clasp onto a set of numbers and run with them despite the warning signs (read footnotes!). And here I want to emphasize a problem with the toolbox of statistics. In math, if you plug random stuff into a calculation, it usually won't work. The equation won't balance, you get irrational numbers, division by zero, an obviously bizzare result, or something. In statistics, when you plug your numbers into the equation, you always get an answer. It is the primary job of the statistician no to do math, it is to understand that data, ask the correct questions, perform the apporpriate tests, and correctly understand their result.
In this study, the authors used a t-test. Also called a student's t-test, and one with great tradition in the alcoholic world, having been invented to help quality control at the Guinness Brewery in the early 1900s. I cribbed the text from wikipedia to show what the test looks like:
 is not a pooled variance. For use in significance testing, the distribution of the test statistic is approximated as being an ordinary Student's t distribution with the degrees of freedom calculated using
is not a pooled variance. For use in significance testing, the distribution of the test statistic is approximated as being an ordinary Student's t distribution with the degrees of freedom calculated usingWrong test, meaningless result, even if it churned out numbers that seemed to make sense. And yes, any freshman in college can tell you this, and anyone who claims to be a wine economist should too. Not that this study is unusual in making this error. You see it all the time in studies about health care policy. But that is another blog entry for a different blog.
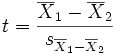
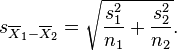
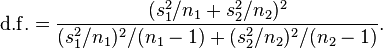
As a social scientist, I often treat ordinal scale data as interval scale data... but doing so means constantly reminding oneself things like "you can't actually have 2.5 children."
ReplyDeleteQuestion: When they say "bang for the buck," is the bang pleasure or resale value? These are related but not identical, and it seems like the paper is also conflating the two. (Not that I read the whole thing.)
ReplyDelete